In this short tutorial I will explain how to computer Discrete Fourier Transform by Example. The reason is simple. It is always easier to understand something new by actually doing, so that's what we will be doing here.
I will be using image transformations as an example. So let's jump into it.
I'm not going to go into much details of what Fourier transform is but rather focus more on actual examples. Here is a really good place to start Discrete Fourier Transform - Simple Step by Step
We know that Discrete Fourier Transform (DFT) goes from spatial(time) domain to frequency domain and vice versa. Going from spatial domain to frequency domain is called forward DFT and going from the frequency domain to spatial domain is called inverse DFT.
Forward Discrete Fourier Transform
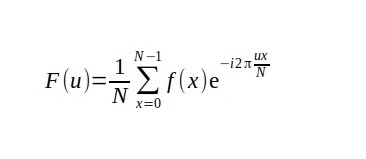
Let's consider a list of real numbers: 36, 22, 45, 15. Thus, we have F = 36, 22, 45, 15. N = 4. u = (0,1,2,3). x = (0,1,2,3). Now let's compute the coefficients for these numbers.
So we have F(u) = u*e^(-i*2*π*u*x/4)
Since x = 0 we get the same number for all numbers.
x = 0: F(0) = (36*e^(-i*2*π*0*0/4) + 22*e^(-i*2*π*0*1/4) + 45*e^(-i*2*π*0*2/4) + 15*e^(-i*2*π*0*3/4)) / 4 = 29.5 + 0i
x = 1: F(1) = 36*e^(-i*2*π*1*0/4) + 22*e^(-i*2*π*1*1/4) + 45*e^(-i*2*π*1*2/4) + 15*e^(-i*2*π*1*3/4) = 36 + 22*cos(-π/2) - 22*i*sin(-π/2) + 45*cos(-π) - 45*i*sin(-π) + 15*cos(-π*3/2) - 15*i*sin(-π*3/2) = 36 + 0 - 45 + 0 + (0i - 22.00i + 0i + 15.00i) = -9/4 + (-7i/4) = -2.25 - 1.75i
x = 2: F(2) = 36*e^(-i*2*π*2*0/4) + 22*e^(-i*2*π*2*1/4) + 45*e^(-i*2*π*2*2/4) + 15*e^(-i*2*π*2*3/4) = 36 + 22*cos(-π) - 22*i*sin(-π) + 45*cos(-π*2) - 45*i*sin(-π*2) + 15*cos(-π*3) - 15*i*sin(-π*3) = 36 - 22. + 45. - 15. + (0i + 0i + 0i + 0i) = 44/4 + (0i/4) = 11 + 0i
x = 3: F(3) = 36*e^(-i*2*π*3*0/4) + 22*e^(-i*2*π*3*1/4) + 45*e^(-i*2*π*3*2/4) + 15*e^(-i*2*π*3*3/4) = 36 + 22*cos(-π*3/2) - 22*i*sin(-π*3/2) + 45*cos(-π*3) - 45*i*sin(-π*3) + 15*cos(-π*9/2) - 15*i*sin(-π*9/2) = 36 + 0 - 45 - 0 + (0i + 22.00i - 0i - 15.00i) = -9/4 + (7i/4) = -2.25 + 1.75i
At this point you can take these coefficients and perform your operations such as filtering, convolution or what have you.
Also now that we have the coefficients we can express them in terms of magnitude and phase.
Magnitude
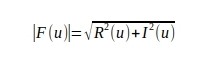
Magnitude tells how much of a certain frequency component is present.
F(0) = sqrt(29.5^2 + 0^2) = 29.50
F(1) = sqrt(-2.25^2 - 1.75^2) = 2.85
F(2) = sqrt(11^2 + 0^2) = 11.00
F(3) = sqrt(-2.25^2 + 1.75^2) = 2.85
Phase
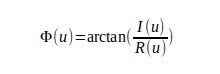
Phase tells where the frequency component is in the image.
Φ(0) = atan2(0 / 29.5) = 0
Φ(1) = atan2(-1.75 / -2.25) = -2.48
Φ(2) = atan2(0 / 11) = 0
Φ(3) = atan2(1.75 / -2.25) = 2.48
Inverse Discrete Fourier Transform
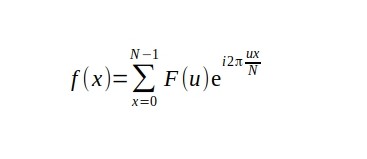
After performing some operations we need to do the inverse.
Now let's reconstruct the list from the coefficients that we just computed.
f(0) = (29.5 + 0i)*e^(i*2*π*0*0/4) + (-2.25 - 1.75i)*e^(i*2*π*0*1/4) + (11 + 0i)*e^(i*2*π*0*2/4) + (-2.25 + 1.75i)*e^(i*2*π*0*3/4) = 29.5 - 2.25 + 11 - 2.25 = 36.00
f(1) = (29.5 + 0i)*e^(i*2*π*1*0/4) + (-2.25 - 1.75i)*e^(i*2*π*1*1/4) + (11 + 0i)*e^(i*2*π*1*2/4) + (-2.25 + 1.75i)*e^(i*2*π*1*3/4) = 29.5 + (-2.25*cos(π/2) + 1.75*sin(π/2) - i*(2.25*sin(π/2) - 1.75*cos(π/2))) + (11.00*cos(π) - 0*sin(π) + i*(11.00*sin(π) + 0*cos(π))) + (-2.25*cos(π*3/2) - 1.75*sin(π*3/2) + i*(2.25*sin(π*3/2) + 1.75*cos(π*3/2))) = 29.5 + 1.75 - 11 + 1.75 = 22.00
f(2) = (29.5 + 0i)*e^(i*2*π*2*0/4) + (-2.25 - 1.75i)*e^(i*2*π*2*1/4) + (11 + 0i)*e^(i*2*π*2*2/4) + (-2.25 + 1.75i)*e^(i*2*π*2*3/4) = 29.5 + (-2.25*cos(π) + 1.75*sin(π) - i*(2.25*sin(π) - 1.75*cos(π))) + (11.00*cos(π*2) - 0*sin(π*2) + i*(11.00*sin(π*2) + 0*cos(π*2))) + (-2.25*cos(π*3) - 1.75*sin(π*3) + i*(2.25*sin(π*3) + 1.75*cos(π*3))) = 29.5 + 2.25 + 11 + 2.25 = 45.00
f(3) = (29.5 + 0i)*e^(i*2*π*3*0/4) + (-2.25 - 1.75i)*e^(i*2*π*3*1/4) + (11 + 0i)*e^(i*2*π*3*2/4) + (-2.25 + 1.75i)*e^(i*2*π*3*3/4) = 29.5 + (-2.25*cos(π*3/2) + 1.75*sin(π*3/2) - i*(2.25*sin(π*3/2 - 1.75*cos(π*3/2))) + (11.00*cos(π*3) - 0*sin(π*3) + i*(11.00*sin(π*3) + 0*cos(π*3))) + (-2.25*cos(π*9/2) - 1.75*sin(π*9/2) + i*(2.25*sin(π*9/2) + 1.75*cos(π*9/2))) = 29.50 - 1.75 - 11 - 1.75 = 15.00
So we got 36, 22, 45, 15. We are getting the same numbers because we didn't make any changes in the frequency domain.
Now let's write a simple python script to compute Discrete Fourier Transforms. Why? Because sometimes it's easier to understand what we are actually doing by looking at the code.
Output:
Coefficients: (29.50, 0.00), (-2.25, -1.75), (11.00, 0.00), (-2.25, 1.75),
Magnitude: 29.50, 2.85, 11.00, 2.85,
Phase: 0.00, -2.48, 0.00, 2.48,
Our List: (36.00, 0.00), (22.00, 0.00), (45.00, 0.00), (15.00, 0.00),
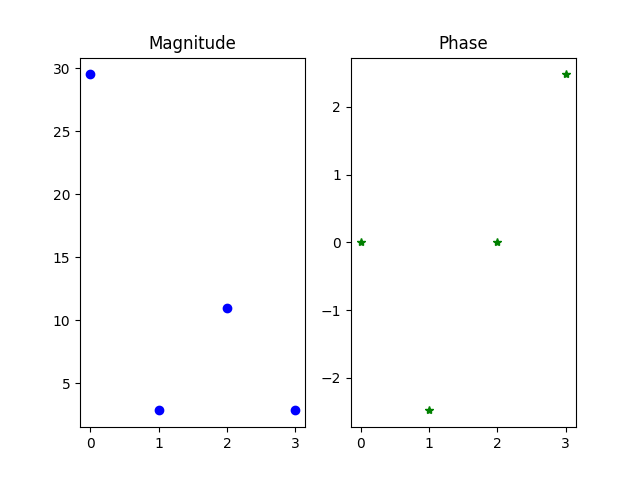
These don't look good because we didn't have a lot of numbers.
And that's it. Next time I will explain how to do Fast Fourier Transform which is super cool.
If you have any questions or I messed up somewhere, please emails me at nikatsanka@gmail.com