In the part 1 of Fourier Transforms by Example we showed how to compute Discrete Fourier Transform which is fairly easy to do, however there is a better and smarter way of computing Fourier Transforms using Fast Fourier Transform (FFT), just a faster algorithm, which is the method used in real world applications.
Again here we aren't going to get into the details on how FFT works, for that here is a really nice explanation The Fast Fourier Transform Algorithm, but it's worth noting how much better it performs over DFT. So, DFT is about θ(n^2) and FFT is about θ(n log n), which is a significant improvement. Keep in mind that this is one of the FFT varients.
Now let's consider the same number list as in part one. 36, 22, 45, 15. One thing we have to remember is that the number of elements has to be a power of 2, and why is that we will see shortly.
As you already know DFT is:
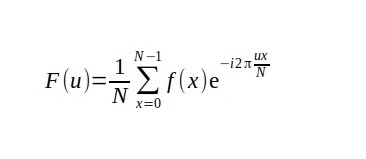
Now let's re-write this: The basic idea is to break up a transform of length N into two transforms of length N/2 using the identity.
Forward FFT
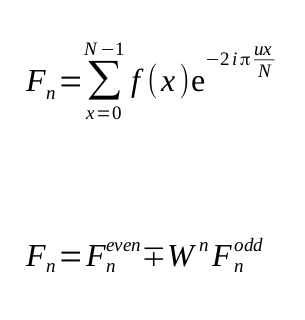
First we group the elements according to even and odd positions, until we are down to a single element. Then when we combine the even and odd indexes. If you don't know what we are doing, watch this The Fast Fourier Transform Algorithm
Now we can start the butterfly computation
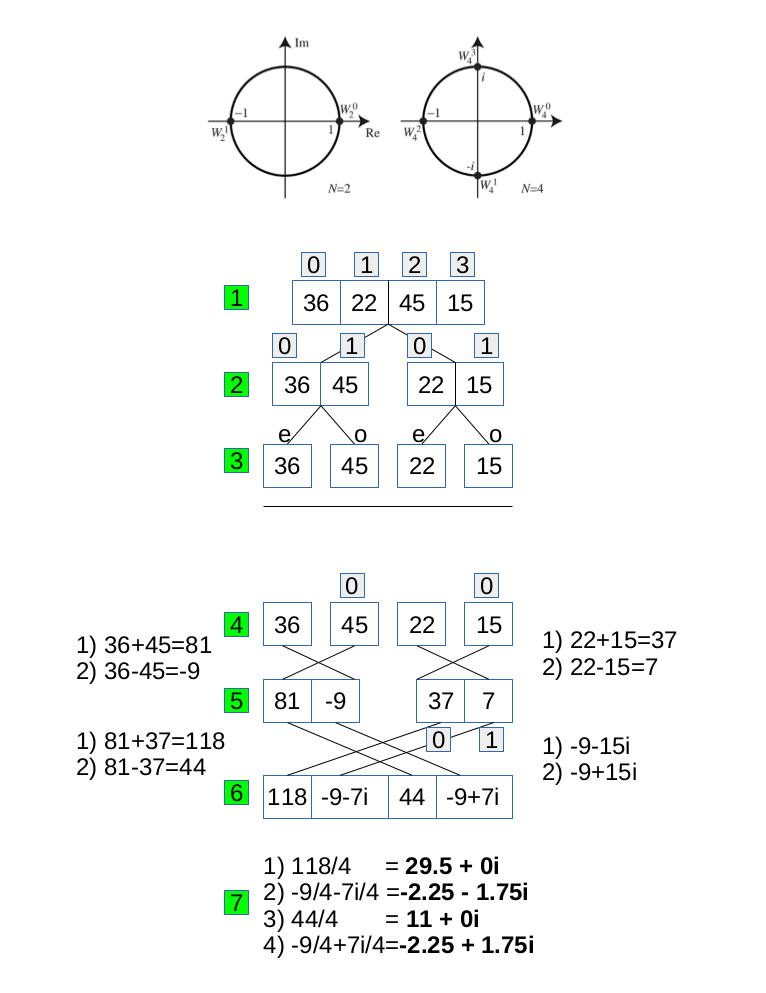
Eplaination:
Steps 1, 2 and 3 are self-explanatory, we are simply regrouping the numbers. Step 4, we take an even and an odd element and start the butterfly computation. At this point we only have 2 elements, thus we have N = 2. We can make things easier if we precomputed weights. Weights are the exponent values that are derived from a unit circle. You can see the pre-computed weights on top. When N = 2, 0th weight will always be 1, so we the same number. Step 5, here N = 4 and when n = 1 we get -i. In the last step we simply divide the results derived in step 5 by N which is 4. And we get the same results as in Part 1 of Fourier Transforms by Example but with far less computation.\
And that's it. Cool right?